5  グラフの作成

これまでに本書の中でもデータのグラフ表現について、いくつかの例とともに紹介してきました。 データをグラフに表現するでは、ヒストグラムと箱ヒゲ図を紹介しました。 2変数のデータの関係を見る際は散布図が有効であることも、相関の中で解説しました。 グラフ表現がデータの要約、比較において優れる点について理解いただけたかと思います。

データ分析の歴史においては、ジョン・スノウによるコレラ死亡者の状態を示す地図やナイチンゲールのくさび形グラフなど、データそのものではなくデータをグラフに表現することが社会を動かす契機となることがありました。 データ可視化はデータの内容を訴える、コミュニケーションのツールとして機能します。

一方で巷には粗悪なグラフも蔓延る点についても知っておかねばなりません。 数式によって導かれる分散や相関係数などとは異なり、グラフは人の意識をもって作成されます。 このとき情報操作のためのグラフが作られないとは限りません。 グラフに示されたデータを見ると、我々は意識せずにそれを受け入れる傾向にあります。 しかし情報を鵜呑みにすることは危険な行為です。

グラフの良し悪しを判断できるようになるためには、数多くのグラフを見ること、審美眼を養うこと、そしてデータ表現について批判できるようになるが重要です。 ここではグラフが示されたときに正しく読み解く能力を身につけるとともに、グラフを作成する立場となった場合に、情報を正しく伝えられるか、誤解を招かない方法について紹介します。

章の中で利用するパッケージを次のコマンドで読み込みます。

library(dplyr)
library(ggplot2)
library(patchwork)
library(palmerpenguins)
library(sf)
library(rnaturalearth)
library(rnaturalearthhires)

また次のコマンドの実行は作図の塗り分けを行う関数を読み込む処理です。 こちらも実行しておきましょう。

source("scripts/color_palette.R")

5.1 探索的データ解析

第二次世界大戦の後、1977年にジョン・テューキーが著書「Exploratory Data Analysis」のなかで探索的データ解析（探索的データ分析）の重要性を説きました。 その内容はいっさいの統計的な計算を介在させずに、データのもつ特徴を視覚化せようとする試みでした。 データ解析の第一歩として、計算を行わずにデータを眺める方法である探索的データ解析を提案したのです。

探索的データ解析はデータ分析の第一歩となるだけでなく、次の一歩を踏み出すためにも役立ちます。 例えば散布図による関係の把握は、回帰モデル構築の足がかりになります。 与えられたデータセットからパターンやトレンドを探すことも分析に用いる手法を検討するのに効果的です。

これまでは数値によるデータ表現との比較としてデータ可視化の方法を見てきましたが、 次に示すのは要約統計量だけでは見えてこないデータの特性について、データ可視化の観点から説明する例となります。

5.1.1 同じ統計量でも異なるグラフ: アンスコムの例

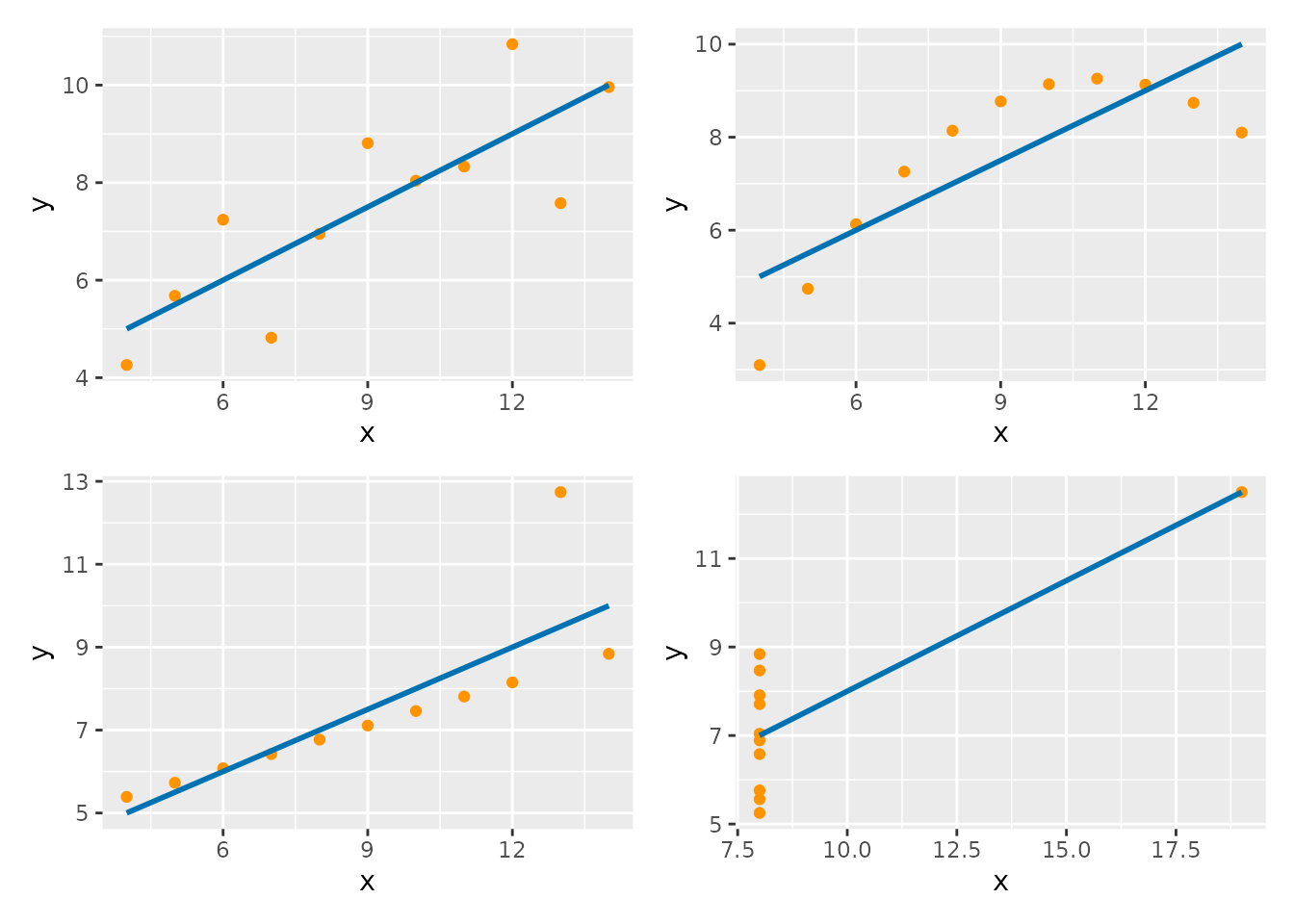
データを直接扱うのではなく、グラフ上に可視化することの重要性を説明する例として、アンスコムの例（アンスコムの数値例）がしばしば用いられます。これは1973年にフランク・アンスコムが紹介したもので、記述統計量や2変数の関係の強さを表す相関係数が小数点第二位まで同じ値となる場合であっても、中身のデータは大きく異なることを示すものです。

表 5.1 にアンスコムが同じ統計量でも異なるグラフを作成する例として示したデータを表示します。

anscombe
表 5.1: アンスコムの例として示される統計量が同じ4種類のデータセット
x1 x2 x3 x4 y1 y2 y3 y4
10 10 10 8 8.04 9.14 7.46 6.58
8 8 8 8 6.95 8.14 6.77 5.76
13 13 13 8 7.58 8.74 12.74 7.71
9 9 9 8 8.81 8.77 7.11 8.84
11 11 11 8 8.33 9.26 7.81 8.47
14 14 14 8 9.96 8.10 8.84 7.04
6 6 6 8 7.24 6.13 6.08 5.25
4 4 4 19 4.26 3.10 5.39 12.50
12 12 12 8 10.84 9.13 8.15 5.56
7 7 7 8 4.82 7.26 6.42 7.91
5 5 5 8 5.68 4.74 5.73 6.89

アンスコムの例を検証してみましょう。 一見異なる値をもつこれらのデータに対して、4種類のデータセットそれぞれで平均と分散、相関係数を求めてみます。

anscombe_long <- 
  anscombe |> 
  tidyr::pivot_longer(
    tidyselect::everything(),
    names_to = c(".value", "set"),
    names_pattern = "(.)(.)")

# 記述統計量（平均と分散）の算出
# setがデータセットの種類を示します
anscombe_long |> 
  group_by(set) |> 
  summarise(across(.cols = c(x, y), .fns = list(mean = mean, sd = sd))) |> 
  summarise(across(.cols = contains("_"), .fns = ~ round(.x, digits = 2)))
Warning: Returning more (or less) than 1 row per `summarise()` group was deprecated in
dplyr 1.1.0.
ℹ Please use `reframe()` instead.
ℹ When switching from `summarise()` to `reframe()`, remember that `reframe()`
  always returns an ungrouped data frame and adjust accordingly.
x_mean x_sd y_mean y_sd
9 3.32 7.5 2.03
9 3.32 7.5 2.03
9 3.32 7.5 2.03
9 3.32 7.5 2.03 
# 同様にデータセットごとに相関係数を求めます
anscombe_long |> 
  group_by(set) |> 
  group_modify(~ tibble::tibble(cor = cor.test(.x$x, .x$y)$estimate)) |> 
  ungroup() |> 
  mutate(cor = round(cor, digits = 2))
set cor
1 0.82
2 0.82
3 0.82
4 0.82

小数点第二位までは同じ値となることが確かめられました。 それでは問題となる散布図を見てみましょう。 2つの変数の直線回帰を行った際の回帰直線も同時に示します (図 5.1)。

anscombe_long |> 
  group_by(set) |> 
  group_map(
    ~ ggplot(.x, aes(x, y)) +
  geom_point(color = course_colors[1]) +
  geom_smooth(method = lm, se = FALSE, color = course_colors[2])) |> 
  wrap_plots(ncol = 2)

図 5.1: アンスコムの例をグラフにしたもの。記述統計量が同じデータであっても散布図にすると見た目が異なる

記述統計量が同じデータセットであっても、散布図の形は異なることが示されました。 また、外れ値が回帰直線に大きく影響している様子も見てとれます。 このようにアンスコムの例は、データを可視化することの重要性だけでなく、外れ値が統計量に与える影響の大きさも示しています。

アンスコムサウルス

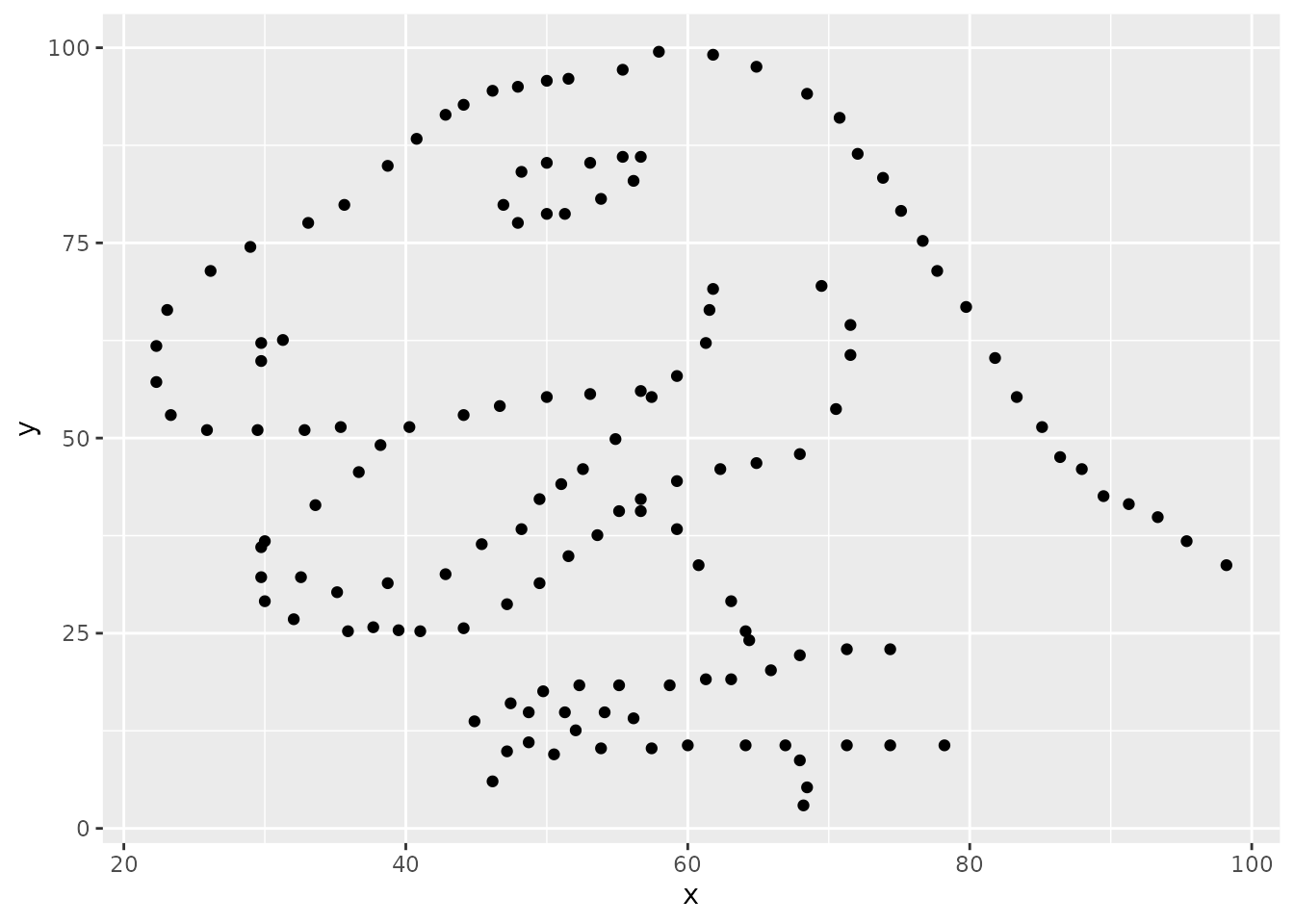
アンスコムの例と同じく、記述統計量が同じでありながら散布図にすると異なる図を描くアルゴリズムをアルベルト・カイロが発見したよ。 これによって生成されたデータの一つを使うと次のような「恐竜」を描くことができるんだ。 この恐竜と同じ記述統計量となるデータを使ってさまざまな散布図が描画できるよ。

library(datasauRus)

datasaurus_dozen |> 
  filter(dataset == "dino") |> 
  ggplot(aes(x = x, y = y)) +
  geom_point()

datasaurus_dozen |> 
  filter(dataset != "dino") |> 
  ggplot(aes(x = x, y = y, colour = dataset)) +
  geom_point() +
  theme(legend.position = "none") +
  facet_wrap(~dataset, ncol = 3)

5.2 分布を示すさまざまなグラフ

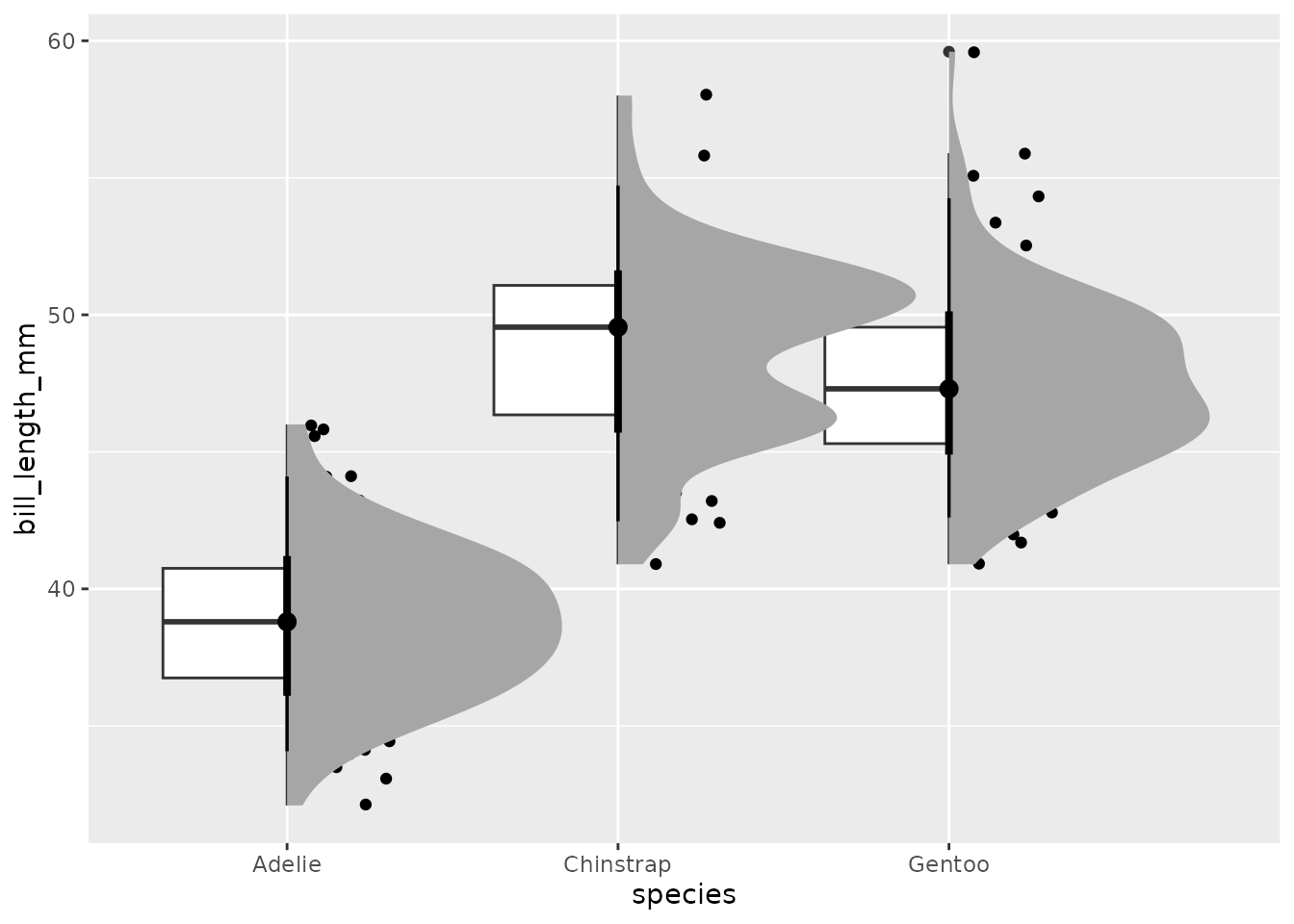
データの分布を示す際、ヒストグラムや箱ヒゲ図から一歩進んだグラフ表現を考えてみましょう。 実際問題として、ヒストグラムや箱ヒゲ図では階級や箱を利用することでデータを効率的に表現できていますが、 個々のデータについては一部の最小値・最大値や外れ値を除いてグラフ表現から無視することになっています。 この問題に対して、代替えとなるいくつかの可視化方法が検証されています。

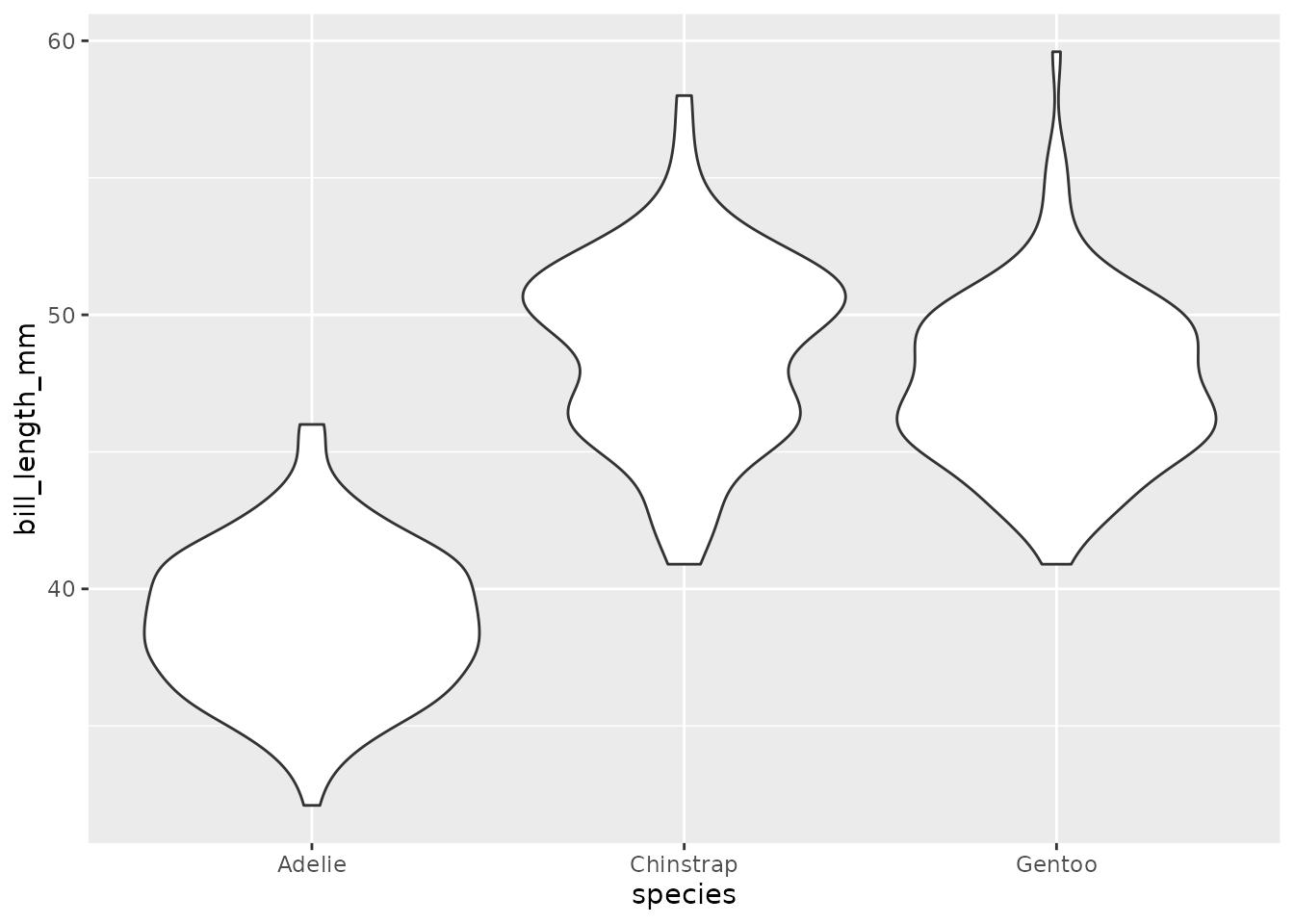
5.2.1 ヴァイオリンプロット

同じ値があるときに横に広がります。

上部の細長い糸巻き部とくびれのある胴部からなるヴァイオリンに似た形をすることがあることから、ヴァイオリンプロットと呼ばれます。

penguins |> 
  ggplot(aes(species, bill_length_mm)) +
  geom_violin()

5.2.2 蜂群図

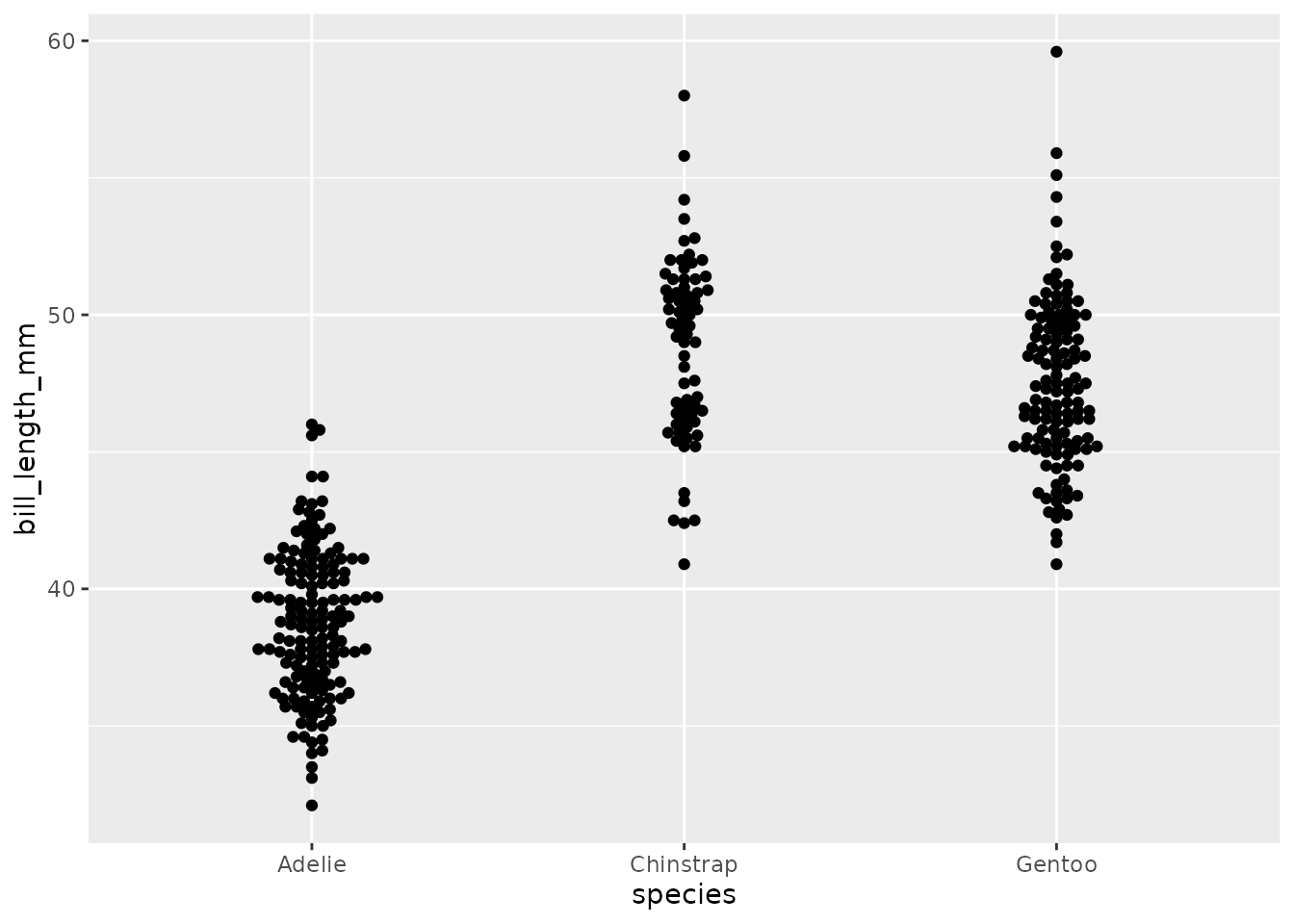
蜂群図（ジッタープロットとも呼びます）はデータの分布の形とそのばらつきを構成する具体的な各値について説明します。 通常、ある質的変数についての量的変数の分布を示すのに用います。 横軸にはデータの値を点として投影します。このとき、もし複数の同じ値があるときには横に広がって表現されます。 点が集まっている様子が蜂の群を連想させることからこの名がついています。

library(ggbeeswarm)
penguins |> 
  ggplot(aes(species, bill_length_mm)) +
  geom_beeswarm()

# ggplot2の標準関数にもgeom_jitter()関数が提供されています
penguins |> 
  ggplot(aes(species, bill_length_mm)) +
  geom_jitter()

5.2.3 雨雲プロット

library(gghalves)
library(ggdist)
penguins |> 
  ggplot(aes(species, bill_length_mm)) +
  geom_half_point() +
  geom_boxplot() + 
  stat_halfeye()

5.3 棒グラフ

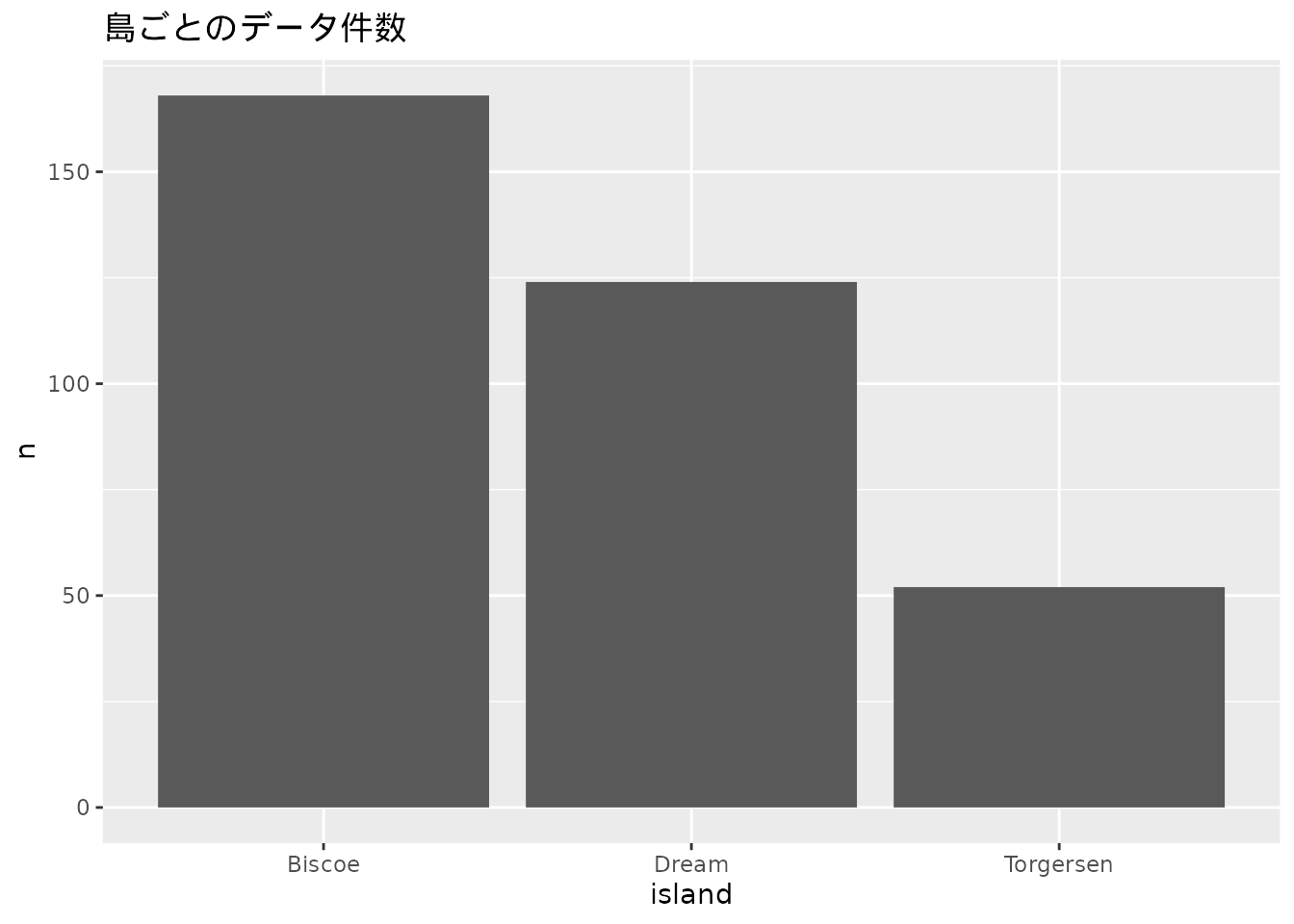
棒グラフ(図 5.2)はデータの大小を棒の高さで表現するグラフの種類です。 そのため、複数の項目間での値の違いを比較するのに適します。

penguins |> 
  count(island) |> 
  ggplot(aes(island, n)) +
  geom_bar(stat = "identity") +
  labs(title = "島ごとのデータ件数")

図 5.2: ペンギンデータにおける島ごとのペンギンの記録数

一般的な棒グラフは横軸に項目を並べ、縦軸に値を配置します。 これにより項目の値がそのまま棒の高さとして利用できます。

棒グラフを作るときは項目の配置に気をつけることが多いです。 まず項目が多い、項目の名前が長い場合には、横軸に項目を並べた際に文字が重なってしまうことがあります。 その際は項目を横並びにするのではなく、縦に配置すると問題を回避できます。 このとき値は縦軸ではなく横軸に置かれます。 つまり軸の縦横を入れ替えて表示します。

もう一つ並びを気にするのは、項目の並びに意味がある場合です。 例えば曜日ごとの値を棒グラフで示すのであれば、その並びは重要です。 月曜日の隣に金曜日が来ていては、見る方が混乱してしまいます。 この場合には月曜日ないし日曜日から始まって（グラフの左端にくる棒）週末が端に来るようにするのが適切です。 同様に、およそ南北に伸びる日本の都道府県や五十音順の項目を扱う際は並びに意味を持たせると良いでしょう。 そうでない場合、データの大きさの順にすると棒グラフが読みやすくなる印象があります。

値が小さいものから大きいものへの並び替えを昇順、 値が大きいものから小さいものへの並び替えを降順と呼びます。 棒グラフの場合、左端がどちらでも良いですが、読む側は左から読み始める（のがほとんど？）ため 右肩下がり・上がりとなるようにすることがあります。

棒グラフを見る・作る際の注意は、原点は0とするのが通常ということです。 原点が0でない棒グラフは誤解を招く恐れがあります。

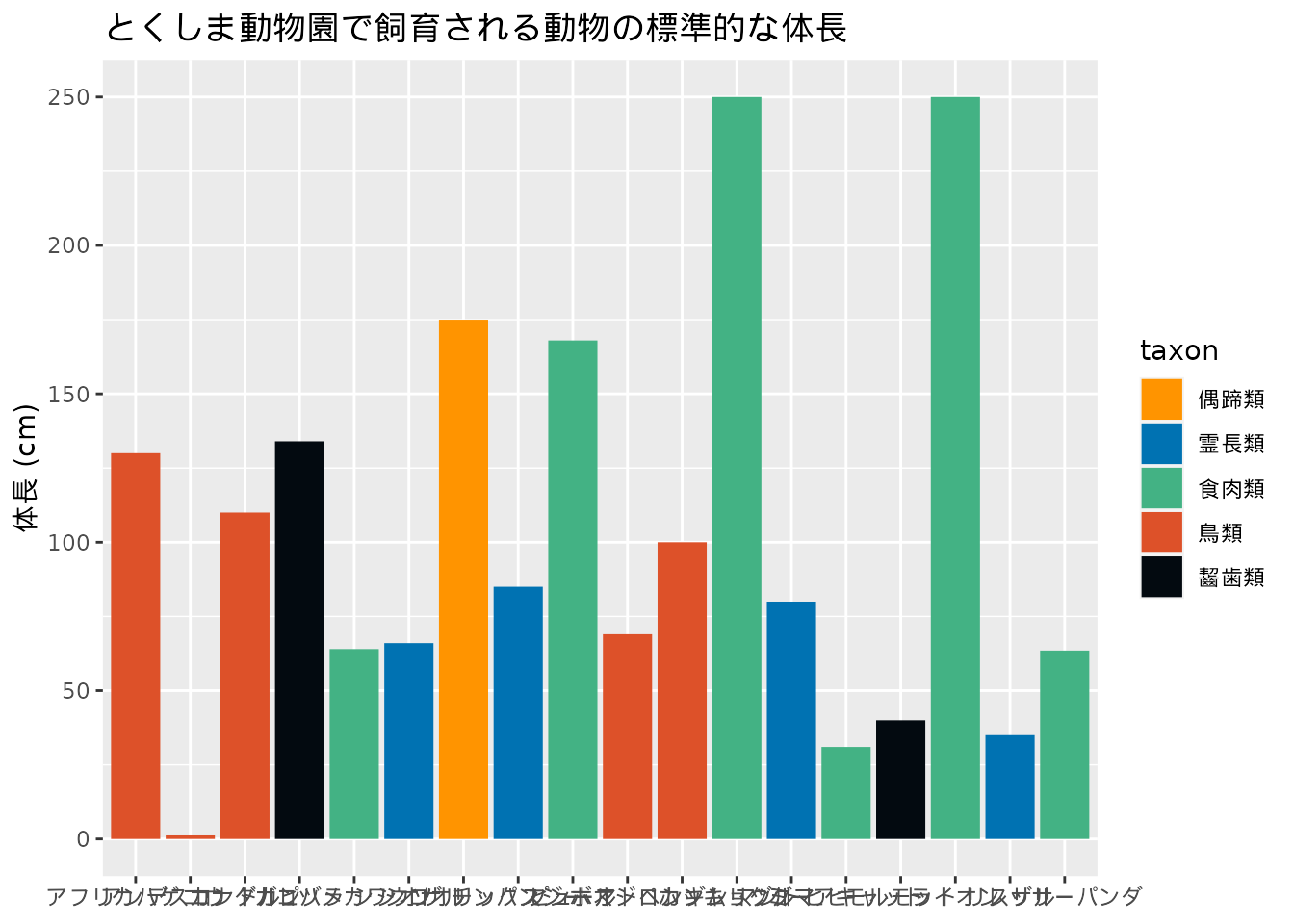
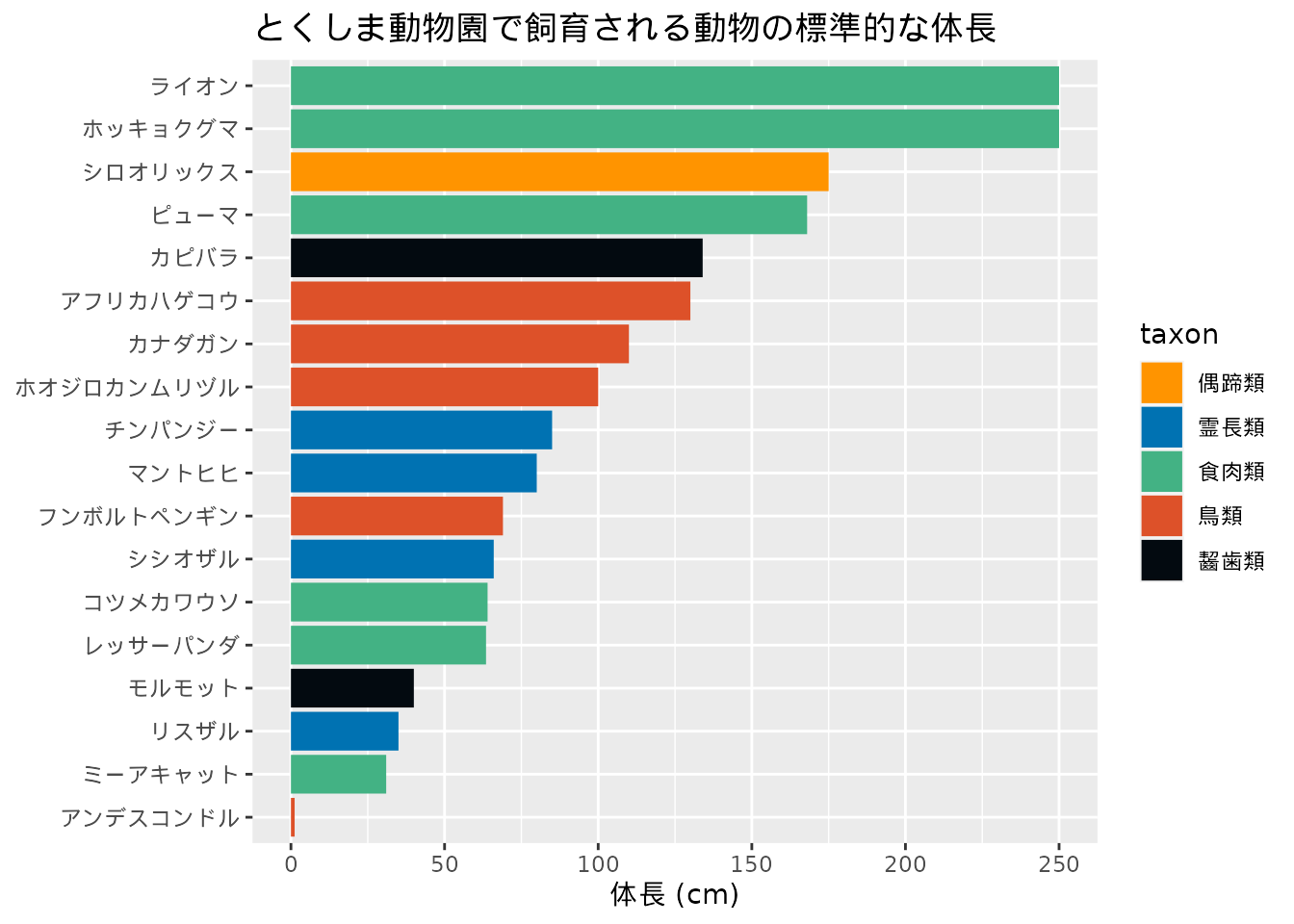
次の棒グラフ(図 5.3)は、いくつかの改善すべき点があります。 グラフを眺めてどのような修正が可能か検討してみましょう。

df_zoo |>
  filter(!is.na(body_length_cm)) |> 
  ggplot(aes(name, body_length_cm, fill = taxon)) +
  geom_bar(stat = "identity") +
  scale_fill_tokupon() +
  xlab(NULL) +
  ylab("体長 (cm)") +
  labs(title = "とくしま動物園で飼育される動物の標準的な体長")

図 5.3: 複数の項目を並べる棒グラフ。項目が多すぎて文字が潰れてしまっています

図 5.4 が修正案です。 このグラフでは項目は横ではなく縦に配置する、項目の並びを工夫するを実践しました。 動物の名前の順序に意味はないので値の大きさで降順に並び替えています。 以上により、前のグラフ (図 5.3) よりも値と項目を眺めることが簡単になったと思います。

df_zoo |>
  filter(!is.na(body_length_cm)) |> 
  ggplot(aes(forcats::fct_reorder(name, body_length_cm), body_length_cm, fill = taxon)) +
  geom_bar(stat = "identity") +
  scale_fill_tokupon() +
  coord_flip() +
  xlab(NULL) +
  ylab("体長 (cm)") +
  labs(title = "とくしま動物園で飼育される動物の標準的な体長")

図 5.4: 棒グラフの改善。

5.3.1 積み上げ棒グラフ

5.4 折れ線グラフ

系列グラフ

主に時系列のデータを扱う際のグラフ表現となります。

横軸に年や月といった時間要素、縦軸にデータの値を投影します。 さらにそれぞれのデータ点を線で繋げることで、データが時系列で変化する様子を表現します。

5.5 円グラフ

円グラフは、グラフに描いた円の中にデータの割合を表すグラフです。 質的変数がもつ割合に対して各値を円の領域（内角）に反映させることで、円全体で100%の構成を表現できます。 円グラフはデータ全体を占める内訳を表現するのに適したグラフです。 つまり、関心のある項目について全体と比較することを念頭にしています。

円グラフは円の真上、時計の12時の位置から円の重心に引いた線を起点として、データの割合を角度で表します。 円の中に占める割合が大きい項目ほど、データの中での割合も多いことを示します。 例えば円グラフの半分、半円を占める値はデータ中の50%の値を意味します。

円グラフを作る場合、起点が12時であること、項目の並びに意味がない場合には値の大きさの順番に配置することが肝心です。

円グラフはデータ可視化の際に棒グラフとともにまず試される図の種類ですが、 円グラフを用いずに棒グラフやその他の方法で示すのが良い場面もあります。 それにはいくつかの理由があります。 第一に円グラフは複数のデータの比較に適さない点が挙げられます。 繰り返しになりますが、円グラフの利点はデータ全体に対する割合を示すことです。 一つの円の中での相対的な比較は可能ですが、別の円グラフを並べたとき、その比較は困難になります。 同様の理由から時系列を扱う場合には円グラフは適しません。 内訳について考えないグラフであれば一般的には棒グラフを選択することを勧めます。

df_zoo |> 
  count(taxon) |> 
  mutate(prop = n / sum(n) * 100) |> 
  ggplot(aes(x = "", y = prop, fill = taxon)) +
  geom_bar(stat = "identity", width = 1) +
  scale_fill_tokupon() +
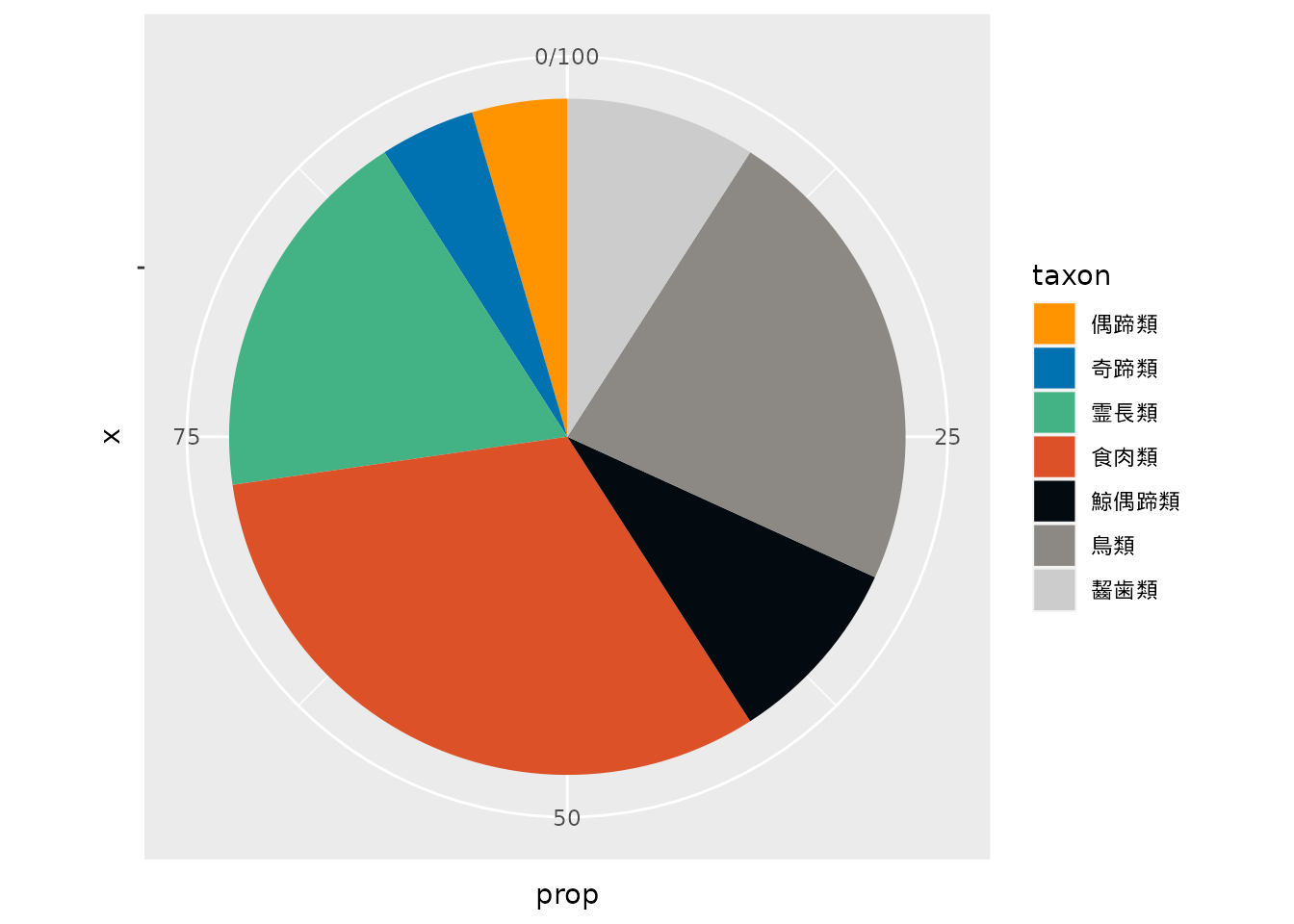
  coord_polar("y")

考えなしに作った円グラフ

このグラフの改善点は

値が大きい順にする

分類群の数は7です。

上位以外の分類群は「その他」としてまとめることにしましょう。 ここではカウントして1種だけしか含まれない「偶蹄類」と「奇蹄類」を「その他」として処理しました。

「その他」は他の項目と違い、複数の項目を混ぜて集計した値です。 そのため円グラフの最後の部分を埋める位置に配置させるが適切です。

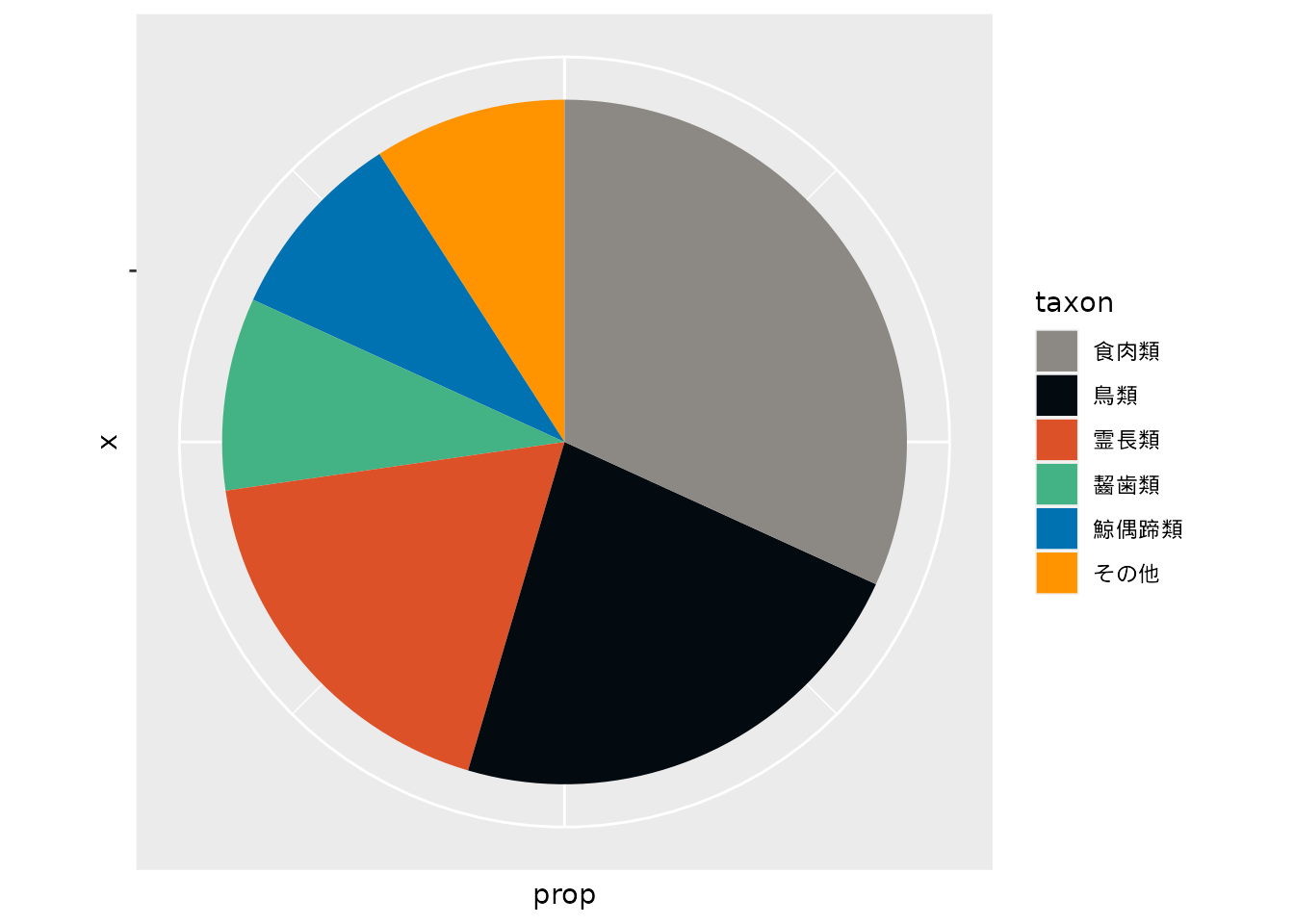
library(forcats)
df_zoo |> 
  mutate(taxon = fct_other(taxon, drop = c("偶蹄類", "奇蹄類"), other_level = "その他")) |> 
  count(taxon) |> 
  mutate(prop = n / sum(n) * 100,
         taxon = fct_rev(fct_relevel(fct_reorder(taxon, n), "食肉類", "鳥類", "霊長類", "齧歯類", "鯨偶蹄類", "その他"))) |> 
  arrange(taxon) |> 
  ggplot(aes(x = "", y = prop, fill = taxon)) +
  geom_bar(stat = "identity", width = 1) +
  scale_fill_tokupon() +
  coord_polar("y", start = 0) +
  guides(fill = guide_legend(reverse = TRUE)) +
  theme(axis.text = element_blank())

3D円グラフはやめよう

5.6 地図表現

カルトグラム

df_countries <-
  countrycode::codelist |>
  select(iso2c, cldr.name.ja) |>
  janitor::clean_names()

ne_world <-
  rnaturalearth::ne_countries(scale = 10, returnclass = "sf") |>
  select(admin, name, pop_est, pop_year, iso_a2, continent)

sf_zoo_conservation <- 
  ne_world |> 
  left_join(df_zoo_conservation |> 
              filter(name == "フンボルトペンギン") |> 
              tidyr::unnest(cols = occ) |> 
              select(code, presence),
            by = c("iso_a2" = "code")) |> 
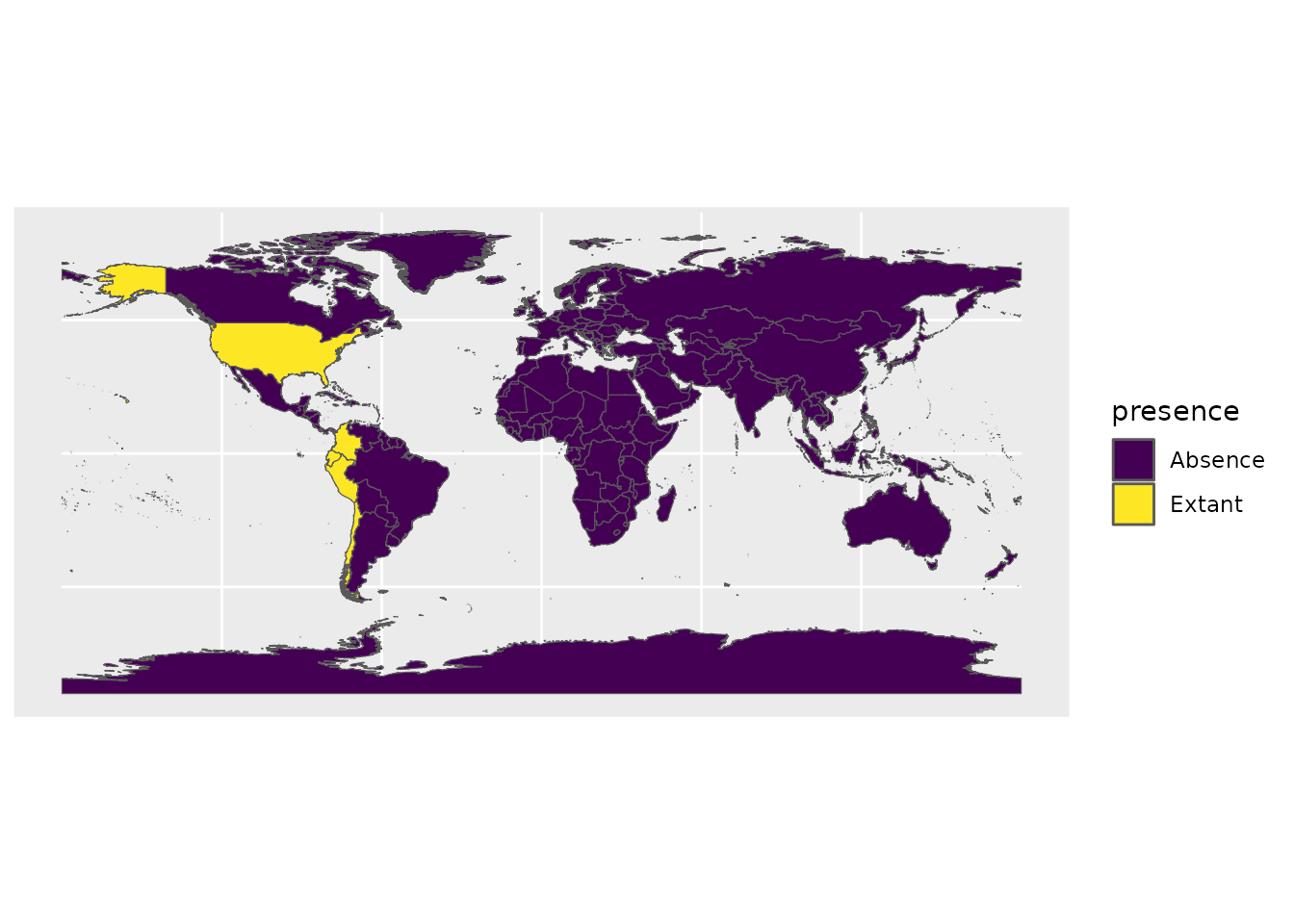
  mutate(presence = tidyr::replace_na(presence, "Absence"))

動物の分布を示す地図を作成してみましょう。

ggplot() +
  geom_sf(data = sf_zoo_conservation, 
          aes(fill = presence), 
          size = 0.001) +
  scale_fill_viridis_d()

library(mapview)
mapview(sf_zoo_conservation, 
                 zcol = "presence")

5.7 まとめと課題

  • さまざまなグラフの種類、グラフを構成する要素を紐解き、示されているデータを理解することができる
  • グラフを作る際には（自分と）他人を騙す行為をしてはいけません
  • ここで紹介したグラフの他に、どんな種類のグラフがあるか探してみよう

5.8 参考文献・URL