相関では2つの量的変数の関係を分析する方法として相関係数や散布図を紹介しました。
回帰とは \(y = f(x)\)
関数によって変数の間の関係を定式化
直線の関数とみなし、\(\hat{Y}_i = a + bX_i\)
変数の関係を理解、
予測ができるようになります。 例として、生まれてからのチンバンジーの日齢と体重
前者の変数が後者の変数に影響していると想定できるため
\(x\)を説明変数、\(y\)を目的変数と呼びます。
変数間の関係、モデルとして組み立てる
モデルによって説明する 直線的な関係を仮定する→線形モデル
単回帰モデル
線形回帰のうち、説明変数が一つの場合を単回帰といいます。 これに対して複数の説明変数によって目的変数の挙動を推定する線形回帰を重回帰と呼びますが、これについては本書では扱いません。 単回帰の基礎を抑えることで、重回帰への理解も深まります。
コード
lm_res <-
lm(weight_kg ~ body_length_cm, data = df_zoo)
lm_res
Call:
lm(formula = weight_kg ~ body_length_cm, data = df_zoo)
Coefficients:
(Intercept) body_length_cm
-72.574 1.324
コード
Call:
lm(formula = weight_kg ~ body_length_cm, data = df_zoo)
Residuals:
Min 1Q Median 3Q Max
-90.587 -37.539 -6.151 25.768 151.495
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -72.5743 26.0890 -2.782 0.0133 *
body_length_cm 1.3243 0.2109 6.280 1.1e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 61.48 on 16 degrees of freedom
(4 observations deleted due to missingness)
Multiple R-squared: 0.7114, Adjusted R-squared: 0.6933
F-statistic: 39.43 on 1 and 16 DF, p-value: 1.098e-05
最小二乗法
回帰直線によって2つの変数の関係をどの程度表現できているかを示す指標
- 回帰直線からの差(残差)
- 残差が小さいほど予測がうまく行っている
残差を2乗し平均をとる –> 残差分散。値が小さいほど回帰直線による予測がうまくいくことを示す
次に示すのは南極大陸に生育するペンギンの大きさを調べた観測データです。 それぞれの変数は次の意味をもちます(詳細は付録のデータセットを参照してください)。
bill_length_mm: 口ばしの長さ。単位はミリメートルbody_mass_g: 体重。単位はグラム
lm()関数
コード
lm_res <-
lm(formula = body_mass_g ~ bill_length_mm, data = penguins)
lm_res
Call:
lm(formula = body_mass_g ~ bill_length_mm, data = penguins)
Coefficients:
(Intercept) bill_length_mm
362.31 87.42
コード
Call:
lm(formula = body_mass_g ~ bill_length_mm, data = penguins)
Residuals:
Min 1Q Median 3Q Max
-1762.08 -446.98 32.59 462.31 1636.86
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 362.307 283.345 1.279 0.202
bill_length_mm 87.415 6.402 13.654 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 645.4 on 340 degrees of freedom
(2 observations deleted due to missingness)
Multiple R-squared: 0.3542, Adjusted R-squared: 0.3523
F-statistic: 186.4 on 1 and 340 DF, p-value: < 2.2e-16
predict()関数
コード
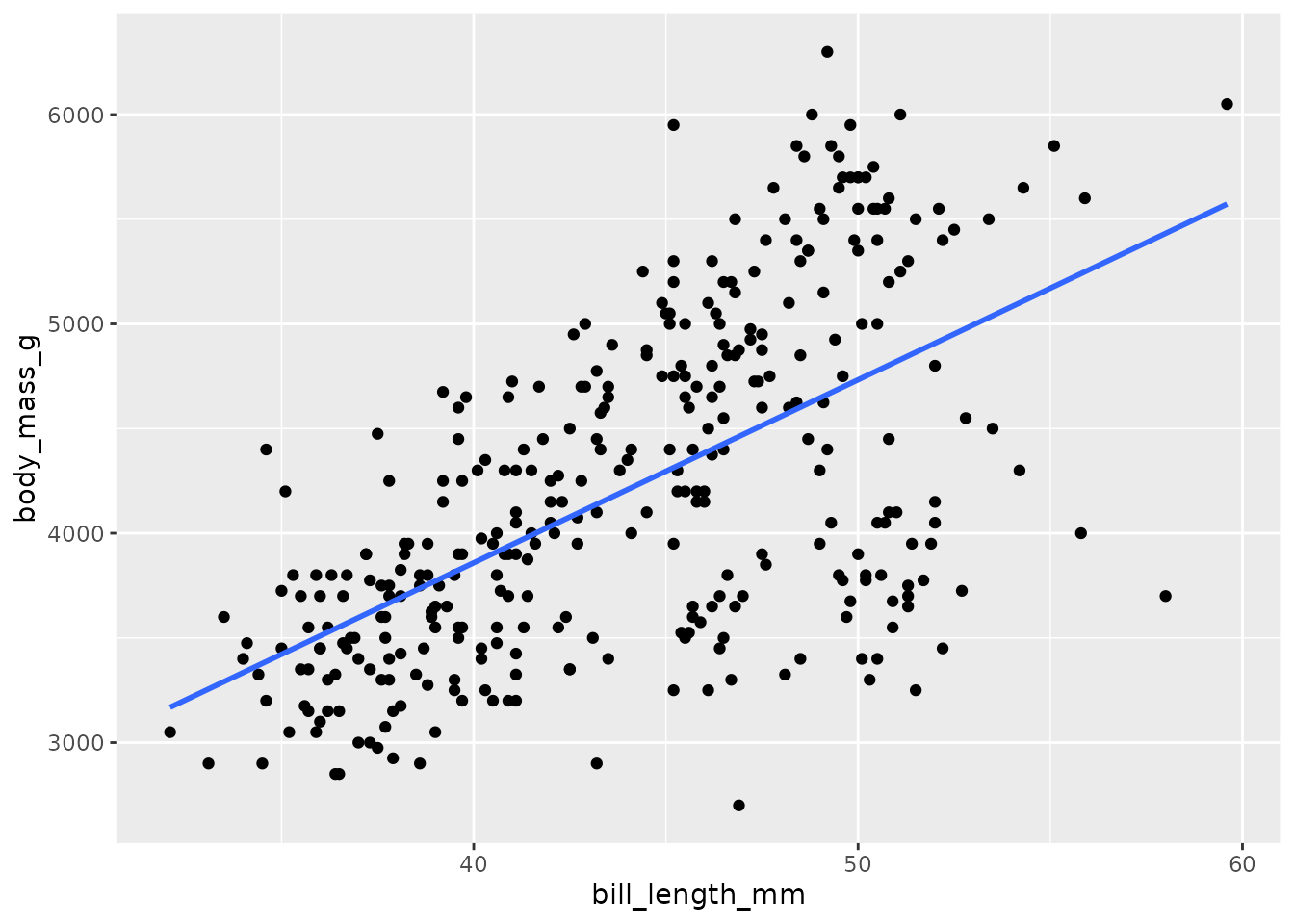
ggplot(penguins, aes(bill_length_mm, body_mass_g)) +
geom_point() +
geom_smooth(method = "lm", se = FALSE)
`geom_smooth()` using formula = 'y ~ x'
Warning: Removed 2 rows containing non-finite values (`stat_smooth()`).
Warning: Removed 2 rows containing missing values (`geom_point()`).
点の配置にもっともよくあてはまる回帰直線は、最小二乗法の原理で求めることができる
データ点に対して、最も適合する直線を引く
二つのパラメータ、切片 \(a\) と傾き \(b\)を決定する
残差 符号の影響を除くために二乗、さらに和をとって残差平方和
決定係数
モデルにおける予測値と実測値との相関係数を2乗した値。
観測値の分散のうち予測によって説明される部分の割合を示す
単純な線形回帰でどのくらい説明できるかを表す値